OM3: An Ordered Multi-level Min-Max Representation for
Interactive Progressive Visualization of Time Series
Yunhai Wang1
Yuchun Wang1
Xin Chen1
Yue Zhao1
Fan Zhang2
Eugene Wu3
Chi-Wing Fu4
Xiaohui Yu 5
1Shandong University
2Shandong Technology and Business University
3Columbia University
4Chinese University of Hong Kong
5York University
Accepted by ACM SIGMOD 2023
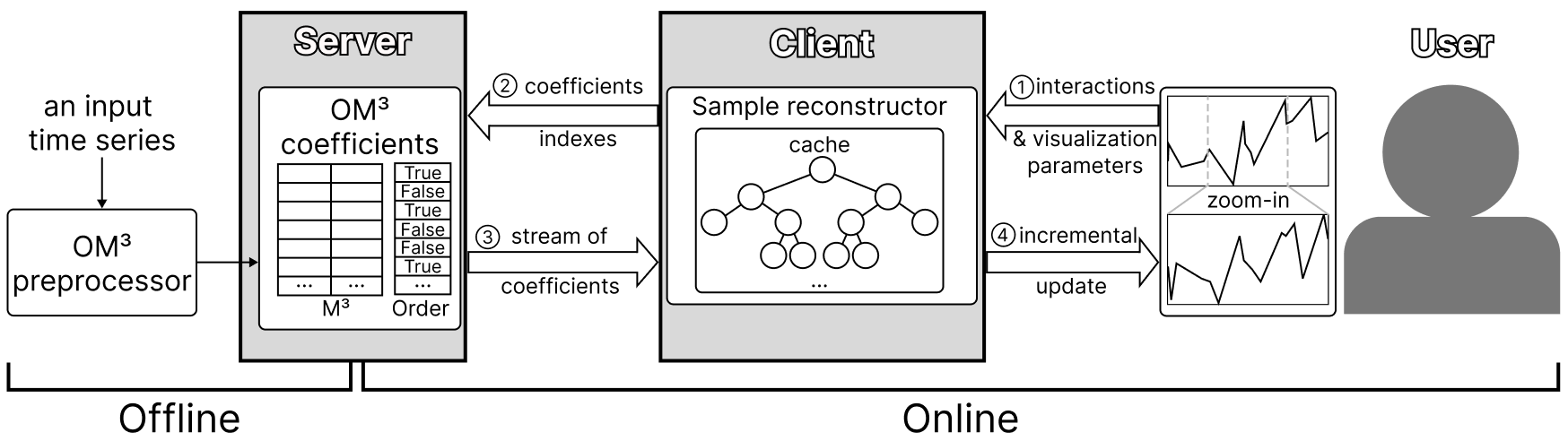
Figure 1:
Our OM3-based architecture for interactive progressive error-free visualization of time series stored.
Abstract:
In this paper, We present a novel multi-level representation of time series called OM3 that facilitates efficient interactive progressive visualization of large data stored in a database and supports various interactions such as resizing, panning, zooming, and visual query. Based on our proposed line-segment aggregation, this representation can produce error-free line visualizations that preserve the shape of a time series in windows of arbitrary sizes. To reduce the interaction latency, we develop an incremental tree-based query strategy to support progressive visualizations, allowing a finer control on the accuracy-time tradeoff. We quantitatively compare OM3 with state-of-the-art methods, including a method implemented on a leading time-series database InfluxDB, in two settings with databases residing either in the local area network or on the cloud. Results show that OM3 maintains a low latency within 300 ms on the web browser and a high data reduction ratio regardless of the data size (ranging from millions to billions of records), achieving around 1,000 times faster than the state-of-the-art methods on the largest dataset experimented with.
Results:
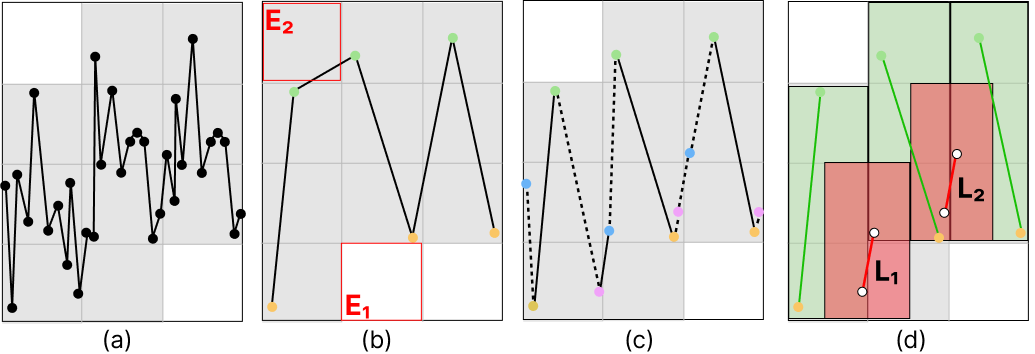
Figure 2: Illustration of Theorem 1. (a) The visualization created by using all data points, where all rasterized pixels are shown in gray; (b) the visualization of the min-max aggregation yields errors of a missing pixel (E1) and a false pixel (E2); (c) the visualization of the M4 aggregation yields the same rasterized pixels as the ones in (a) but the dotted line segments are redundant and unnecessary; and (d) all pixels are correctly set by first rasterizing the lines defined by the min-max aggregation result in each pixel column (in green) and then rasterizing the indispensable inter-column lines (L1) between adjacent pixel columns.
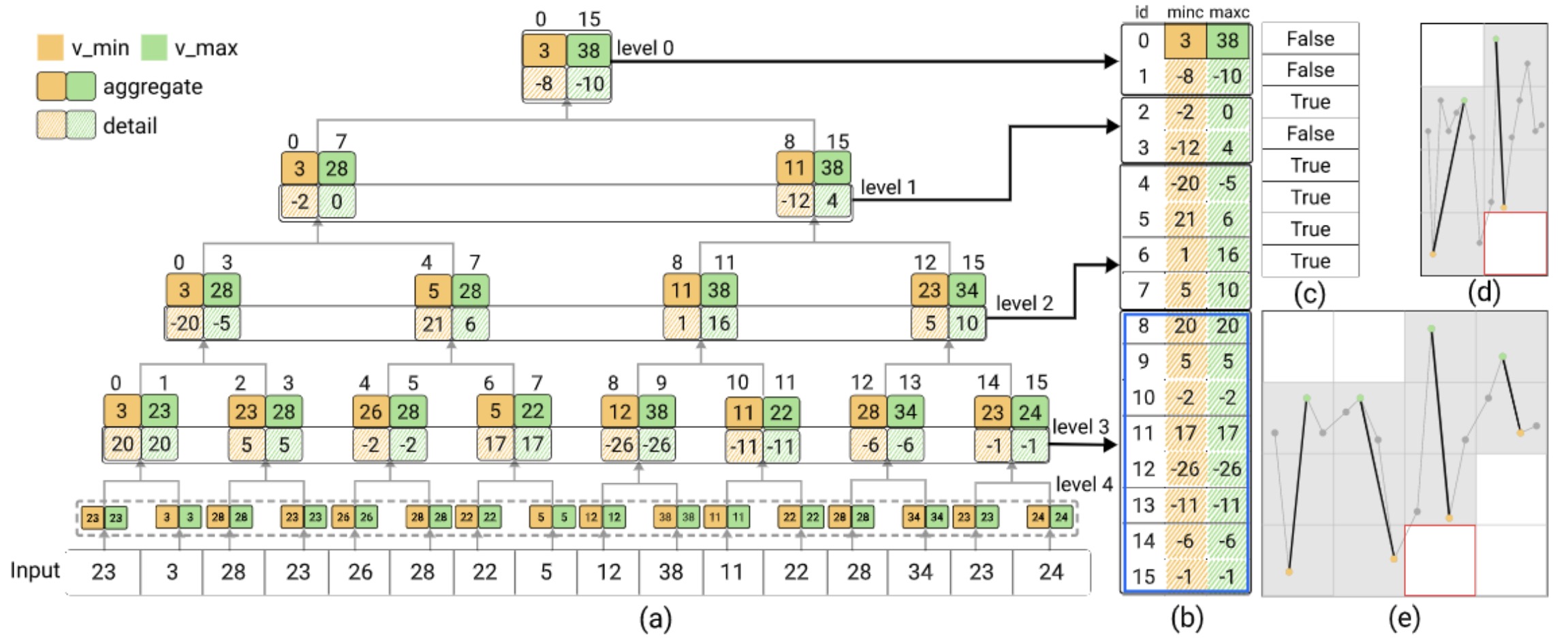
Figure 3: Illustrating the OM3 forward transform and the coefficients stored in the database. (a) The input data (bottom) with 16 samples is recursively transformed to build the four-level coefficient tree. Each tree node has two aggregate coefficients and two associated detail coefficients. To start, we replicate the input data twice to construct the coefficients at level 4, marked by the dotted box. (b) The initial database table stores the final two aggregate coefficients at the top (level 0) and all detail coefficients from the forward transforms; detail coefficients that are redundant for reconstructing the original data are marked by the blue box. (c) The additional database table stores all ordering coefficients. (d,e) Line visualizations (in black) reconstructed by the inverse transform from the aggregate coefficients on a two-pixel-wide window (d) and a four-pixel-wide window (e), where the pixels with the red boxes are missed.
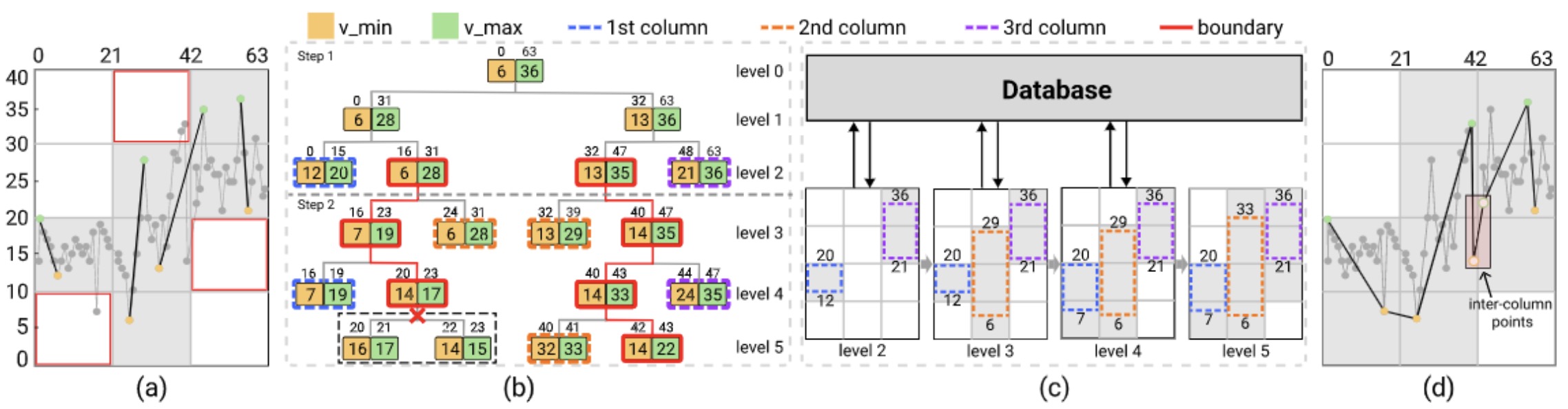
Figure 4: Illustrating how incremental tree-based query supports for accurately visualizing a time series on a three-pixel-width window. (a) Simply generating the visualization by using four groups of the aggregate values at the level 2 could easily miss pixels (red boxes). (b,c) Our query method with pruning can efficiently visit necessary nodes in the OM3 coefficient tree to locate the minimum and maximum aggregates for each pixel column in the target window level by level and uses these value ranges to rasterize the pixel columns in (c). (d) The final visualization produced by our method (grey pixels) is error-free; its rasterization precisely matches the data points in the original line chart. Here, the detail coefficients of the node [14,17] do not need to be loaded, since its value range is covered by the value ranges of the adjacent two pixel columns [7,20] and [6,29], while the inter-column line highlighted in (d) corresponds to the node [14,22].
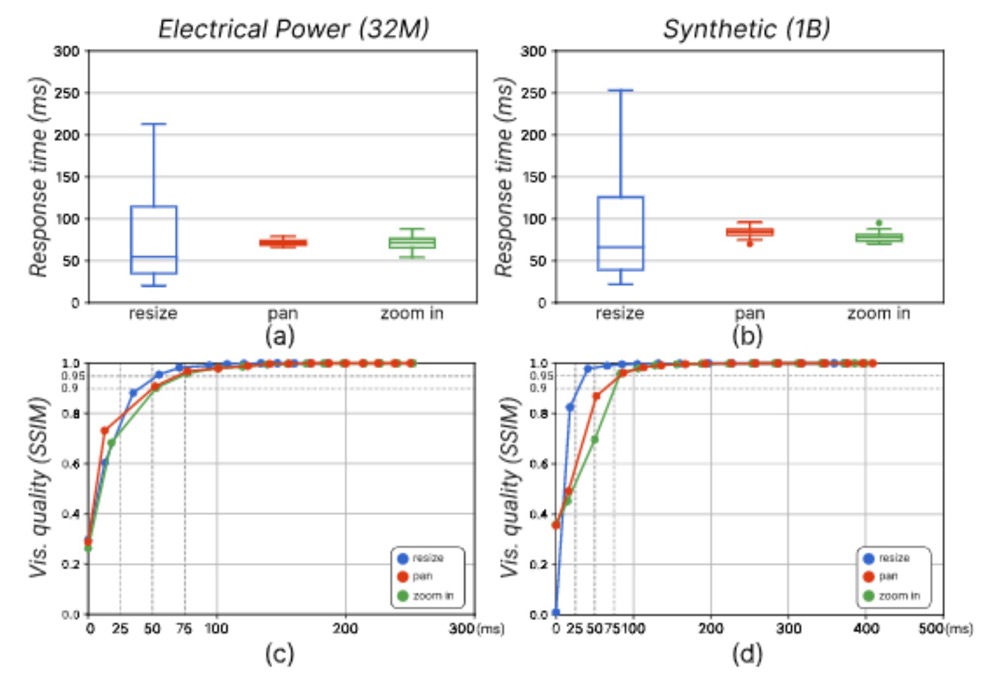
Figure 5: (a,b) Boxplots summarize the response time of 20 trials for producing visualizations with SSIM values larger than 0.95 after performing three interactions on the two datasets. (c,d) The line charts show how SSIM-based visualization quality evolve over the response time for a randomly selected trial for each interaction on the two data.
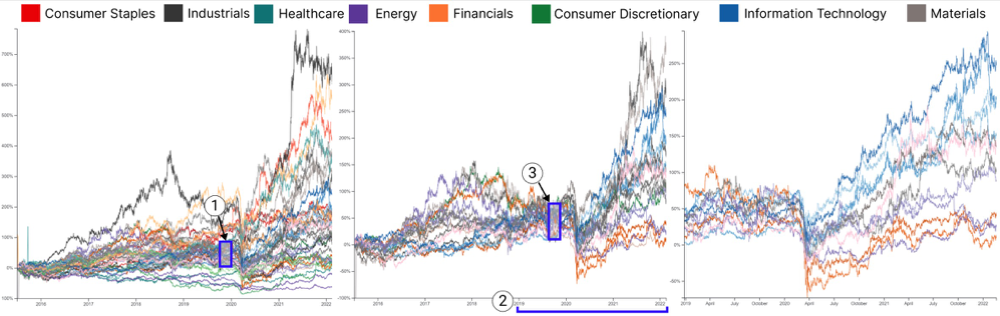
Figure 6: 44 stock price lines visualized using OM3 , exhibiting heavy visual clutter. Hence, we put the timebox marked by the blue box to filter out the stocks with different behaviors and produce the visualization shown in (b). (c) Further, we zoom into a specific time interval between 2019 and 2022 and then use a timebox to further filter the stocks.
Materials:
 |
 |
| Paper | Supp. |
Acknowledgements:
The authors would like to thank the fruitful discussions with Dominik Moritz and André Kohn.
This work was supported by the grants of the National Key R&D Program of China (2022ZD0160805),
NSFC (No. 62132017, 62141217), NSERC, and NSF (No. 1845638, 2008295, 2106197, 2103794), as well as Amazon and Adobe.